Conceptos básicos
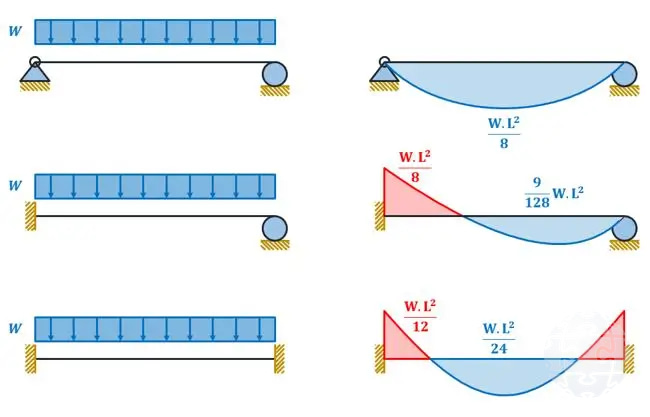
Figura 1. Influencia de las condiciones de apoyo en la respuesta estructural y distribución interna y externa de fuerzas.
Influencia de la condición de apoyo en el sistema estructural
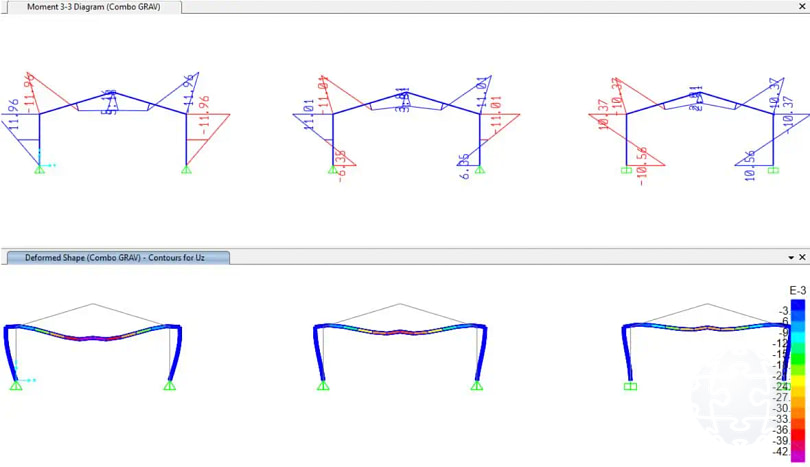
Figura 2. Influencia de las condiciones de apoyo tanto en la distribución de fuerzas como de deformaciones para el caso de cargas gravitacionales.
Las estructuras metálicas, debido a su flexibilidad inherente, son susceptibles a problemas de deformación y a la amplificación de fuerzas flectoras debido a imperfecciones durante el montaje. Esto conlleva a la aparición de efectos de segundo orden, conocidos como efectos P-D. Por esta razón, el código AISC 360 establece procedimientos detallados de análisis por estabilidad en su capítulo C. Es fundamental un control preciso de las deformaciones laterales para un diseño óptimo en estructuras metálicas.
La restricción lateral en estas estructuras puede generar diferencias significativas en las fuerzas. En la Figura 3 se ilustra la disparidad en las fuerzas flectoras y los desplazamientos entre las diferentes hipótesis de apoyo bajo una misma carga lateral.
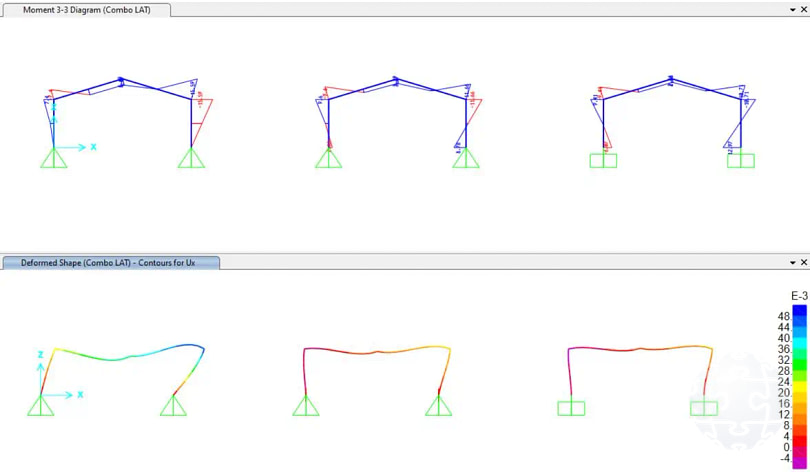
Figura 3. Influencia de las condiciones de apoyo en la distribución de fuerzas como de deformaciones para el caso de cargas laterales.
Ejemplo: Hipótesis de base Flexible
Una práctica común en ingeniería estructural es despreciar la capacidad rotacional de las placas base, dejando al sistema estructural la total responsabilidad de soportar las fuerzas flectoras y controlar las grandes deformaciones resultantes en esta hipótesis. En este caso, los sistemas de sujeción o placas base suelen diseñarse únicamente para fuerzas axiales y cortantes, lo que generalmente resulta en espesores delgados y, por lo tanto, flexibles.
Sin embargo, aunque se desprecie esta rigidez en el modelo de cálculo del framing estructural y las placas base posean cierta rigidez acorde con la hipótesis planteada, en realidad estas placas son capaces de absorber momentos en función de su rigidez. Por lo tanto, su capacidad debe ser analizada en función de los niveles de momentos que pueden soportar.
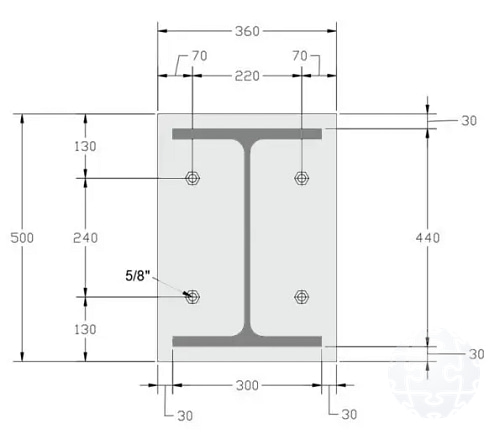
Figura 4. Configuración de placa base en estudio con hipótesis de base flexible.
Análisis de unión (base flexible) con IDEA Statica
Si efectuamos un análisis de esta conexión mediante el software IDEA Statica CONNECTION, que permite llevar a cabo un análisis tensional mediante elementos finitos y evaluar la rigidez de la conexión, obtendremos los resultados mostrados en la Figura 5:
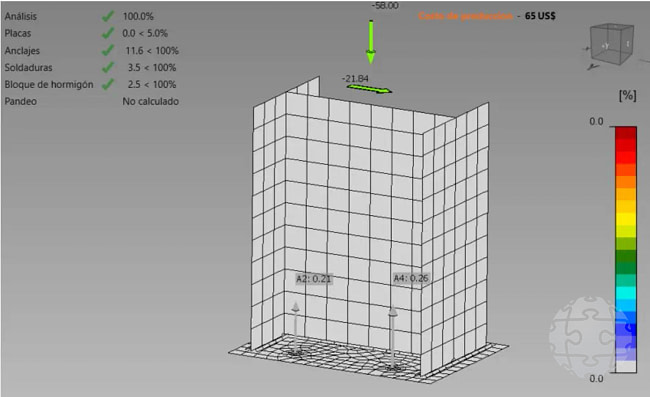
Figura 5. Verificación de deformaciones plásticas en IDEA Statica CONNECTION.
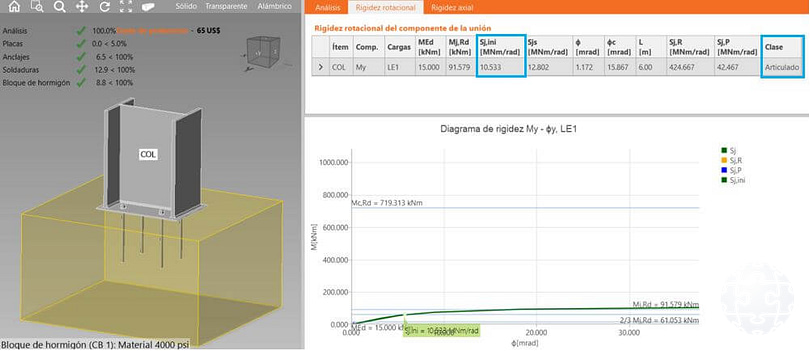
Figura 6. Análisis de rigidez flexional en IDEA Statica CONNECTION para plancha base con hipótesis de base flexible.
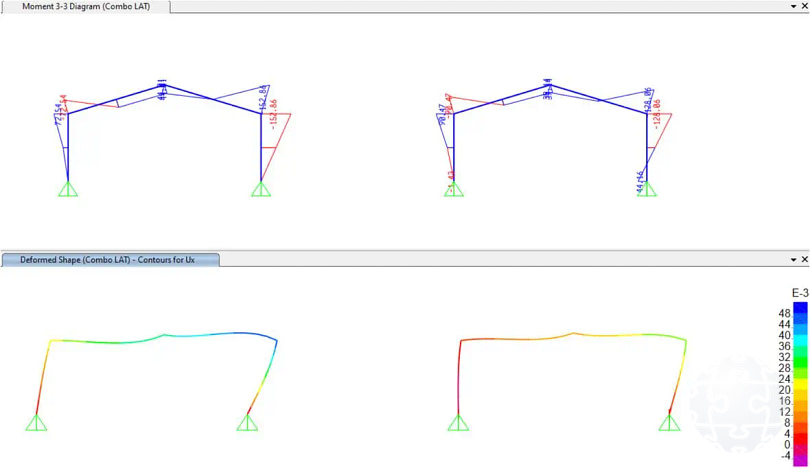
Figura 7. Incorporación y evaluación de la rigidez flexional en el modelo matemático de cálculo.
Al introducir los nuevos valores de momentos y cortantes determinados en el análisis estructural y verificar la conexión (Figura 4) en IDEA Statica, se observa en la Figura 8 que la unión falla. Esto indica que solo puede soportar el 50% de las cargas determinadas en el análisis estructural. Por lo tanto, es necesario reconsiderar la configuración de la unión o aumentar el espesor de la placa base.
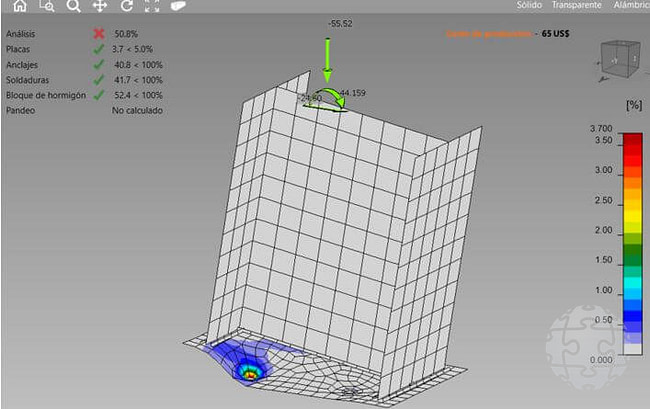
Figura 8. Evaluación de los estados de deformación plástica de la plancha base ante las nuevas solicitación obtenidas con la corrección de rigidez en la base.
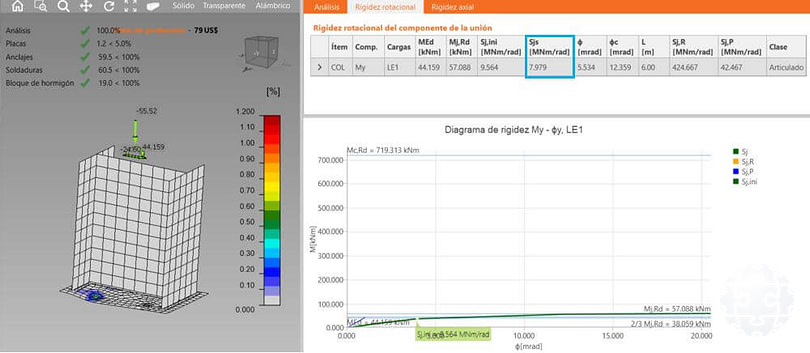
Figura 9. Determinación de rigidez flexional de la plancha base con 10 mm de espesor.
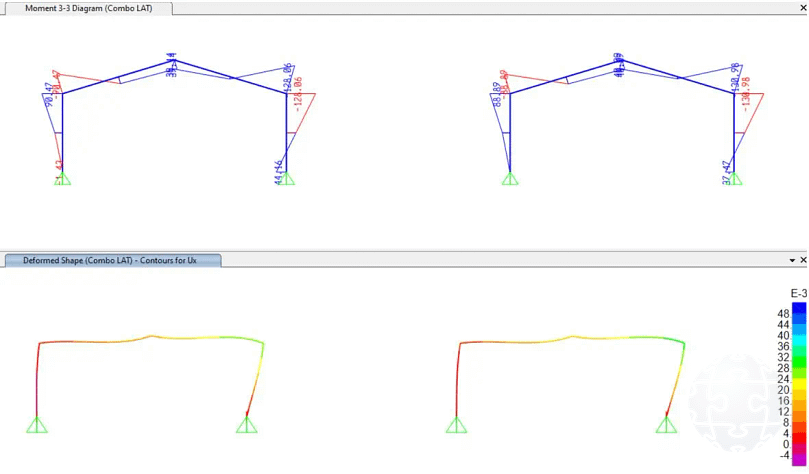
Figura 10. Respuesta estructural con la nueva rigidez secante determinada.
Ejemplo: Hipótesis de base Rígida
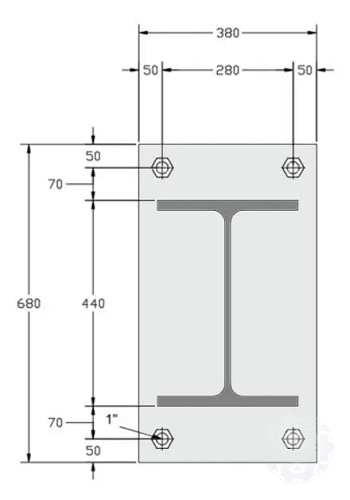
Figura 11. Configuración de plancha base en estudio con hipótesis de base rígida.
Análisis de unión (base semi-rígida) con IDEA Statica
Al realizar el chequeo de deformaciones plásticas y el análisis de rigidez rotacional mediante el software IDEA Statica CONNECTION, se obtienen los resultados que se muestran en la Figura 12. Se evidencia una holgura notable en la capacidad de la placa base analizada. Además, se obtiene una rigidez inicial de 89.578 MN.m/rad, la cual es significativamente superior al caso de hipótesis de base flexible. Sin embargo, a pesar de esto, la unión no se clasifica como "rígida", sino como "semi-rígida".
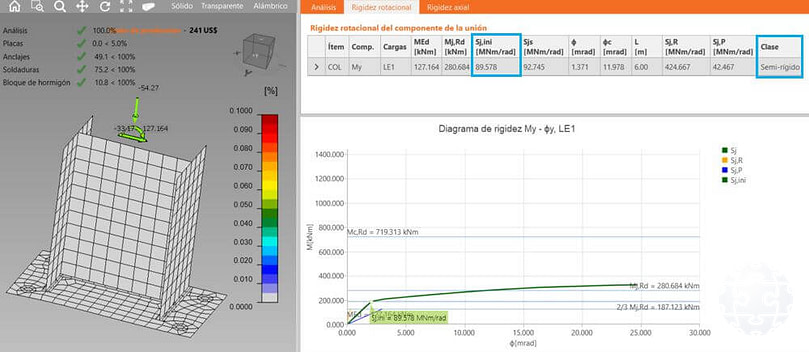
Figura 12. Análisis de deformaciones plásticas y de rigidez flexional en IDEA Statica CONNECTION para plancha base con hipótesis de base rígida.
Basándonos en los resultados obtenidos, se lleva a cabo una reevaluación estructural incorporando la rigidez determinada para la unión. Los resultados del análisis se presentan en la Figura 13.
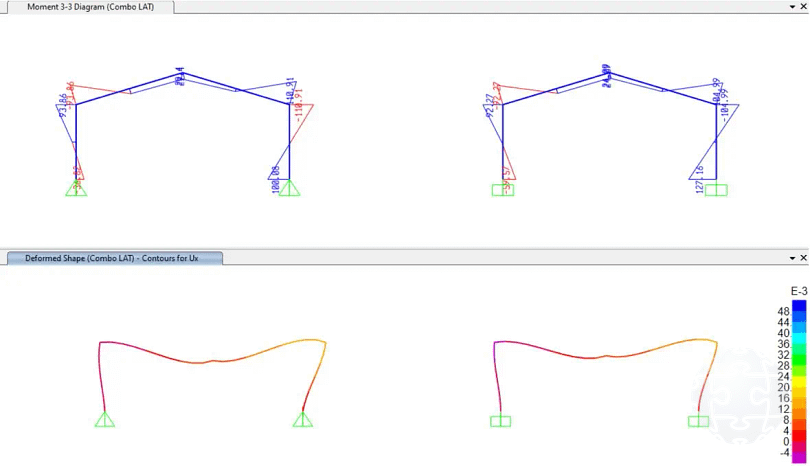
Figura 13. Análisis estructural considerando la rigidez obtenida para el caso de base semi-rígida.
Optimizando el espesor de la plancha base mediante un proceso iterativo se obtiene un espesor de 20 mm, con una rigidez rotacional de 47.138 MN.m/rad (Figura 14).
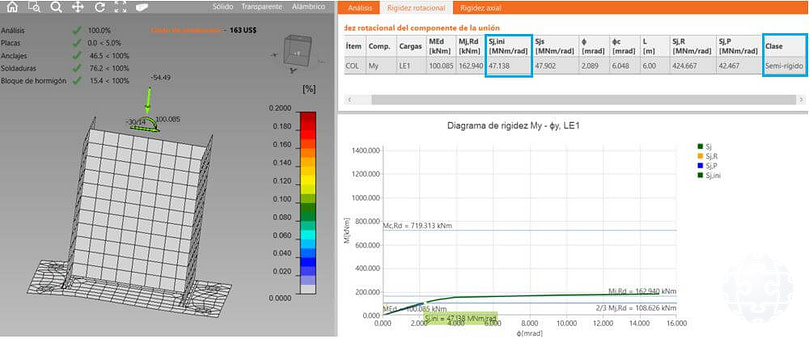
Figura 14. Análisis de deformaciones plásticas y de rigidez flexional en IDEA Statica CONNECTION para plancha base con hipótesis de base semi-rígida con optimización de espesor.
Por último, se incorpora esta nueva rigidez en el modelo matemático para validar los resultados.
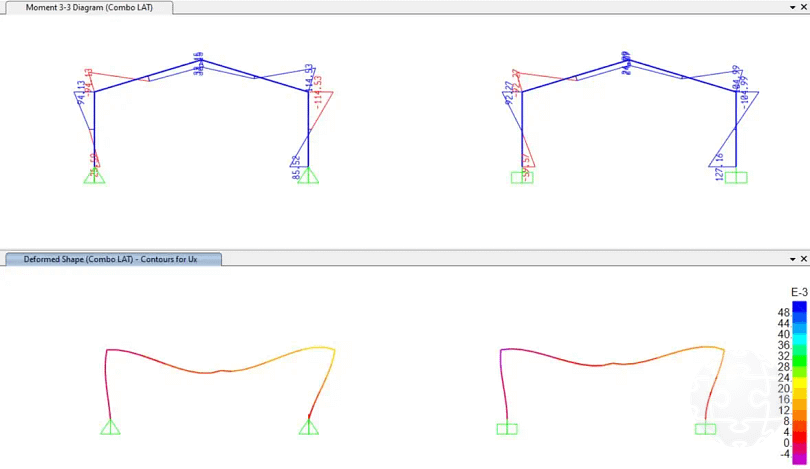
Figura 15. Análisis estructural considerando la rigidez obtenida para el caso de base semi-rígida con optimización de espesor.
Influencia de la incorporación de rigidizadores en la rigidez flexional de planchas base
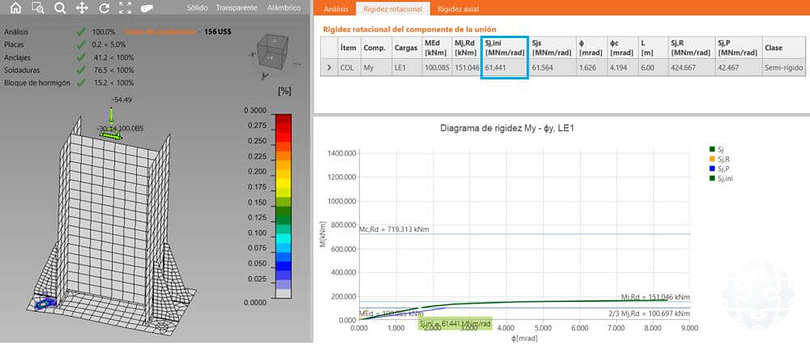
Figura 16. Influencia de la incorporación de rigidizadores en la rigidez flexional de planchas base.
Referencias
• American Institute of Steel Construction, Specification for structural steel buildings (ANSI/AISC 360-22), Chicago, IL, 2022.
• Bruneau M., Uang C. and Sabelli R. Ductil Design of Steel Structures, 2nd Edition, The McGraw Hill, Inc., 2011.
• Fisher J. and Kloiber L. Steel Design Guide N°1 - Base Plate and Anchor Rod Design, 2nd Edition, American Institute of Steel Construction.
El Curso proporciona al participante los criterios y procedimientos a seguir para desarrollar proyectos típicos de Edificaciones Industriales mediante aplicación de normativa internacional, manejo de software de última generación y discusión de casos reales.

