¿Cómo diseñar zapatas para turbinas eólicas Onshore?
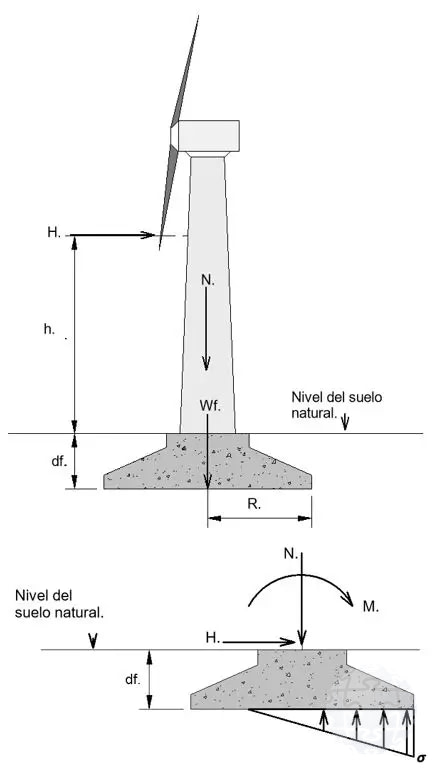
Figura 1: Descripción de los mecanismos principales de transferencia de carga de la turbina a la cimentación.
Normativas aplicables al diseño geotécnico y estructural
¿Qué enfoques de diseño estructural existen para zapatas de turbinas eólicas?
Método clásico de la viga en voladizo
Procedimiento general de aplicación para el método clásico
Con la finalidad de ilustrar el procedimiento general para efectuar el diseño estructural de zapatas de turbinas eólicas utilizando el enfoque de la viga en voladizo, se indica un esquema general de aplicación (Ver figuras 2 y 3).
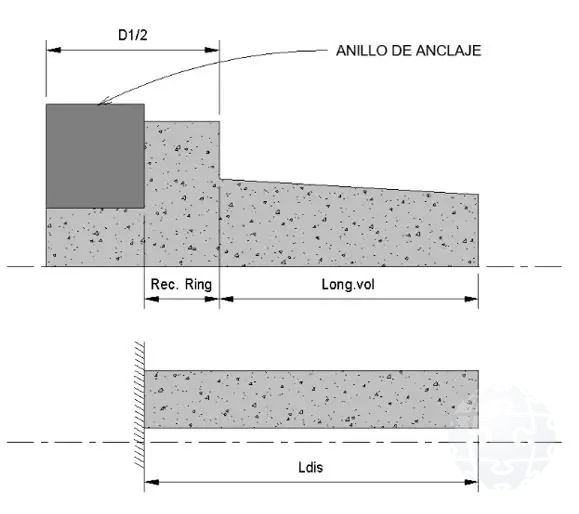
Figura 2: Esquema de la viga en voladizo para diseño de zapata de turbina eólica Onshore.
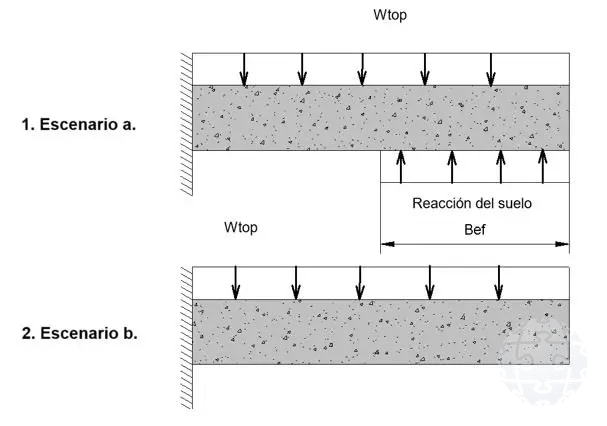
Figura 3: Escenario de carga.
Método del puntal tensor (Strut and Tie Model, STM)
El método del puntal-tensor es especialmente útil para el diseño de "Regiones D" (zonas de discontinuidad) en elementos de concreto reforzado. Estas zonas se caracterizan por manifestar un comportamiento no lineal debido a concentraciones de esfuerzos, cambios bruscos de geometría, aplicación de cargas concentradas o presencia de aberturas.
El STM modela la trayectoria de esfuerzos en la estructura como un sistema de puntales (compresión) y tensores (tracción) interconectados mediante nudos.
Este enfoque está respaldado por normativas de diseño estructural tales como el IEC 61400-6:2020 (anexo k), ACI 318-25 (capítulo 23 con apoyo del reporte ACI PRC 445) y el Eurocódigo 2 (EN-1992) Diseño de estructuras de concreto (clausula 6.5).
En la Figura 4 se observa un planteamiento conceptual del recorrido general de puntales y tensores de una zapata de una turbina eólica Onshore.
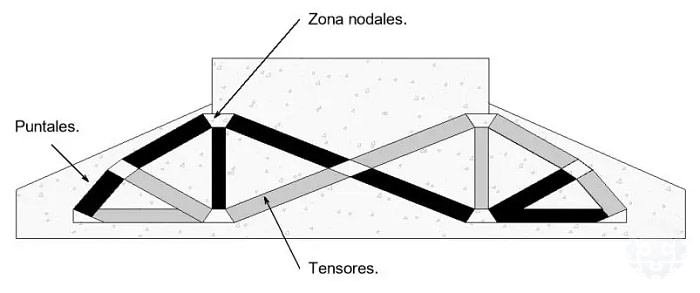
Figura 4: Representación del método del puntal-tensor para diseño de zapata de turbina eólica Onshore.
Procedimiento general de aplicación para el método del puntal-tensor
Con la finalidad de ilustrar el procedimiento general para diseñar la zapata de una turbina eólica Onshore mediante el método del puntal-tensor, se indica un esquema general de aplicación (Ver Figuras 5 y 6).
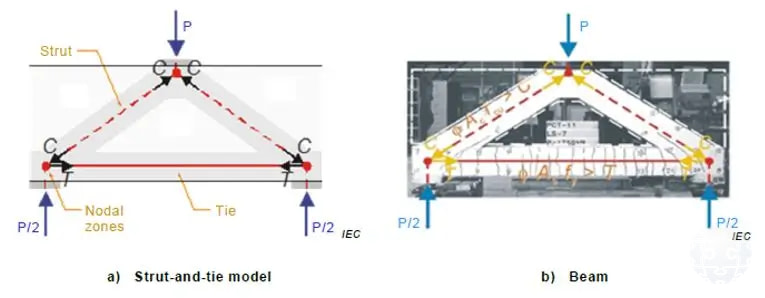
Figura 5: Ejemplo de diseño de una viga alta utilizando el método del puntal-tensor (IEC 61400-6:2020 © IEC 2020).
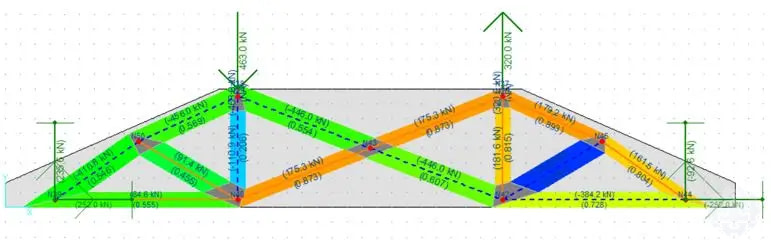
Figura 6: Modelo puntal tensor para zapata onshore (CAST Universidad de Illinois).
¿Cómo se modelan las cargas actuantes sobre zapatas de turbinas eólicas Onshore?
Tipos de cargas consideradas
En este tipo de proyectos deben evaluarse diferentes acciones sobre la cimentación:
- Cargas gravitacionales: peso propio de la turbina y componentes mecánicos.
- Cargas de funcionamiento.
- Cargas extremas ambientales: viento y sismo.
De esta forma, al analizar la zapata se debe considerar el efecto conjunto de cargas verticales (compresión y/o tracción) y fuerzas debidas a momentos de volcamiento actuando en la base de la estructura.
Modelos de estimación
- Se pueden estimar mediante modelos integrales MEF en 3D, en los que se modela la turbina junto con el sistema suelo-cimentación.
- No suelen ser desarrollados por el proyectista de la cimentación debido a la complejidad de calibración de parámetros y de aspectos relacionados con el funcionamiento de componentes mecánicos de la propia turbina que típicamente son controlados por el fabricante.
- Habitualmente, estos modelos los desarrolla el fabricante de la turbina para validar el diseño definitivo y efectuar simulaciones completas de funcionamiento, luego que se ha efectuado un análisis detallado del sistema suelo-cimentación.
Obtención de cargas
En la práctica, el proyectista a cargo del diseño de la cimentación recibe del fabricante de la turbina las cargas esperadas sobre la cimentación:
- Cargas gravitacionales estáticas.
- Cargas dinámicas.
- Momentos de volcamiento.
Con estas cargas:
- Primero se verifica el comportamiento geotécnico de la cimentación con las dimensiones propuestas.
- Posteriormente se desarrolla el diseño estructural, considerando la acción combinada de cargas verticales y momentos de volcamiento actuando en la base de la turbina.
Descomposición de cargas
Las cargas verticales son consideradas de forma directa sobre el modelo, mientras que las fuerzas debidas al efecto de los momentos de volcamiento sobre zapatas típicamente se obtienen mediante descomposición de tales momentos en pares de fuerzas (compresión/tracción) que luego son distribuidas a puntales y tensores.
Esto se logra mediante el uso de expresiones simplificadas en las que la ubicación de tales fuerzas dependerá del diámetro de la placa circular ubicada en la base de la turbina.
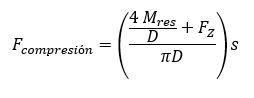
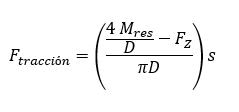
Donde:
- Mres : Momento de volcamiento extremo resultante actuando en la parte superior del ancho de cimentación (kN-m).
- Fz : Fuerza vertical (kN).
- D : Diámetro externo de la placa circular (m).
- S : Espaciamiento radial (m). Los planos radiales tendrán un espesor (s), que equivalente al espaciamiento promedio entre pares adyacentes de varillas de acero.
En la Figura 7 se ilustran las variables requeridas para estimar las máximas componentes de compresión y tracción sobre la zapata:
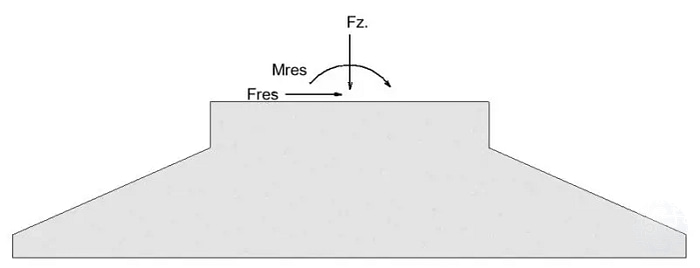
Figura 7: Cargas de diseño sobre la cimentación.
En la Figura 8 se observa un esquema de las componentes de compresión y tracción sobre la zapata, obtenidas al descomponer el momento flector actuando en la base de la turbina.
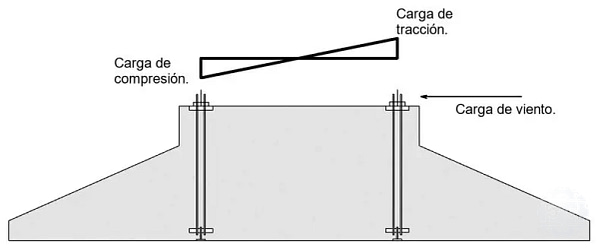
Figura 8: Esquematización de transferencia de carga.
Ejemplo: Diseño estructural de zapata para turbina eólica onshore con el método del puntal-tensor
Geometría y condiciones
Con la finalidad de ilustrar el impacto en el diseño, se realizó el análisis de una zapata de una turbina eólica Onshore mediante el método del puntal-tensor. Para ello se considera el modelo de una zapata circular cuya geometría, cargas y dimensiones se basan en el trabajo de Muzofa T. (2017) “Optimisation of Wind Turbine Foundations" (Figura 9).
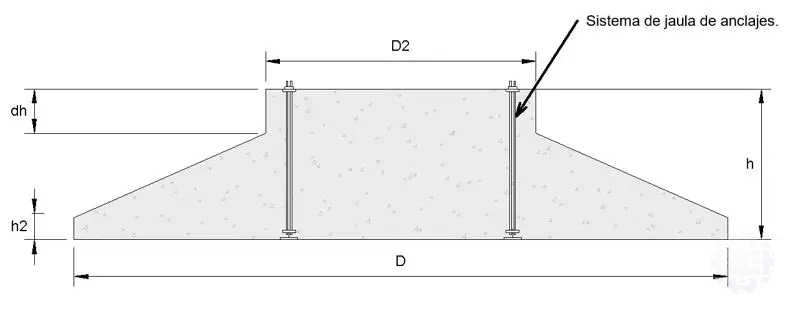
Figura 9: Geometría de la cimentación. Adaptado de Muzofa T (2017).
El análisis del conjunto de puntales y tensores propuestos en la zapata se ha efectuado según lo indicado en el código IEC 61400-6:2020 (anexo k), y el diseño estructural se ha efectuado siguiendo los lineamientos dados por el código ACI 318-25 con apoyo en el reporte ACI PRC 445.2-21 y efectuando una comparación con Eurocódigo 2 (EN 1992-1-1:2004).
Es importante destacar que según el contexto geográfico del proyecto el diseño estructural puede efectuarse según cualquier otro código estructural que contemple dicha metodología.
Procedimiento general de diseño de puntales y tensores
Con la finalidad de ilustrar el procedimiento de cálculo, se ha seleccionado el tensor T1 y el puntal P1 mostrados en la Figura 10.
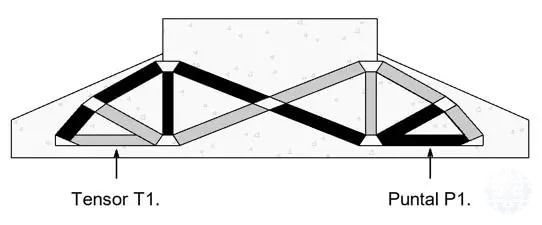
Figura 10: Identificación de elementos del modelo de puntal tensor.
Se estima el acero de refuerzo requerido para ambos elementos por espacio radial (S = 110 mm) (ver Figura 11). A partir de esta configuración se reportan los resultados según los enfoques dados en el ACI y el EN 1992-1-1:2004.
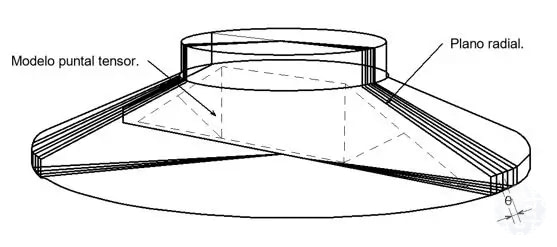
Figura 11: Concepto de espacio radial
Enfoque americano (ACI)
La ecuación para estimar el acero de refuerzo en los tensores según ACI 318-25 (Art. 23.7.2) y tabla 21.2.1:
As = Ft / Φfy
La ecuación para estimar el acero de refuerzo en un puntal, considerando la tracción en un campo de compresión según ACI Reporte 445.2-21 y FIB MODEL CODE 1999, es la siguiente:
Ftp = 0.20 Fp
As = Ftp / Φfy
Donde:
- Ft : Fuerza de tracción en los tensores obtenida del análisis estático (kN).
- Fp : Fuerza en el puntal obtenida del análisis estático (kN).
- fy : Esfuerzo de cedencia (MPa). Considerado en este ejemplo fy = 420 MPa.
- Φ : Coeficiente de reducción de resistencia para el método del puntal tensor.
- Ftp : Fuerza de tracción en el puntal (kN).
Enfoque EN 1992-1-1:2004
La ecuación para estimar el acero de refuerzo en los tensores según el Eurocódigo 2 es la siguiente:
As = Ft / fyd
Donde:
- fyd : Esfuerzo de cedencia de diseño según Eurocódigo 2. Se calcula según la Figura 3.8 del Eurocódigo 2 (MPa). Considerado en este ejemplo fyd = 434.78 MPa.
La ecuación para estimar el acero de refuerzo en un puntal, considerando la tracción en un campo de compresión para una discontinuidad total según el Eurocódigo 2 (Ec.6.59), es la siguiente:
Ftp = 1/4 (1-0.7a/H) Fp
As = Ftp / fyd
Donde:
- Ftp : Fuerza de tracción en el puntal (kN).
- Fp : Fuerza en el puntal obtenida del análisis estático (kN).
- a : Ancho del nodo (mm).
- H : Longitud del puntal (mm).
Espacio radial
El cálculo del espacio radial se realiza a través de una relación trigonométrica, expresada mediante la siguiente expresión:
s = r θ
Donde:
- r : Radio de la torre en la base (mm).
- 𝜽 : Ángulo entre las líneas centrales de planos radiales adyacentes (º).
Acero de refuerzo mínimo
El refuerzo mínimo por retracción y temperatura tiene como propósito limitar la fisuración derivada de los cambios de volumen del hormigón, asociados tanto a la retracción como a las variaciones térmicas.
La cuantía mínima puede estimarse de acuerdo con lo establecido en el ACI 318 o en el ACI 350 para el contexto americano, en el Eurocódigo 2 (EN 1992-1-1:2004) para el contexto europeo, o siguiendo las recomendaciones de diversos investigadores en el marco del método del puntal–tensor.
En este artículo se han adoptado los criterios del ACI 350-20, el cual establece que, para elementos con espesores superiores a 600 mm, no se requiere una cuantía de refuerzo mayor que la definida para un espesor de 600 mm.
Resultados
En la Tabla 1 se reporta el diseño del tensor T1 y el puntal P1 (Figura 11) según ambos enfoques (ACI vs EN 1992-1-1:2004).
Tabla 1: Diseño de acero de refuerzo longitudinal por espacio radial (Figura 10) (S=110 m): Tensor T1 y Puntal P1 (Figura 11).
Enfoque | Elemento | As por espacio radial (mm²/m) |
|---|---|---|
ACI | Tensor T1 | 348.8 |
ACI | Puntal P1 | 218.7 |
EN 1992-1-1:2004 | Tensor T1 | 242.7 |
EN 1992-1-1:2004 | Puntal P1 | 189.4 |
Luego de calcular la cantidad de refuerzo requerida por espacio radial para cada elemento estructural (puntales y tensores inferiores y superiores, según corresponda), es posible obtener un estimado de la cuantía media de refuerzo por metro lineal en el lecho superior e inferior de la zapata (Ver tabla 2).
Tabla 2: Requerimiento de acero de refuerzo longitudinal.
Enfoque | Zona | Cuantía de refuerzo longitudinal media (mm²/m) | Cuantía mínima de refuerzo longitudinal media (mm²/m) |
|---|---|---|---|
ACI | Lecho inferior de la zapata | 3598 | 1781 |
ACI | Lecho superior de la zapata | 3866 | 1781 |
EN 1992-1-1:2004 | Lecho inferior de la zapata | 3225 | 2827 |
EN 1992-1-1:2004 | Lecho superior de la zapata | 3373 | 2827 |
La diferencia en la cantidad de refuerzo requerida entre los enfoques de diseño americano (ACI) y europeo (Eurocódigo) obedece principalmente a que cada normativa emplea distintos factores de diseño, es decir, el ACI utiliza un factor de reducción de resistencia específico para el método de puntal-tensor, mientras que el Eurocódigo considera factores parciales sobre los materiales. Adicionalmente, existe una ligera diferencia en el valor considerado en el ejemplo para el esfuerzo de cedencia del acero entre ambos enfoques.
Finalmente, las Figuras 12 y 13 presentan un detalle referencial del armado de la zapata, derivado de los resultados obtenidos mediante el método de puntal–tensor y de las directrices establecidas en el presente artículo.
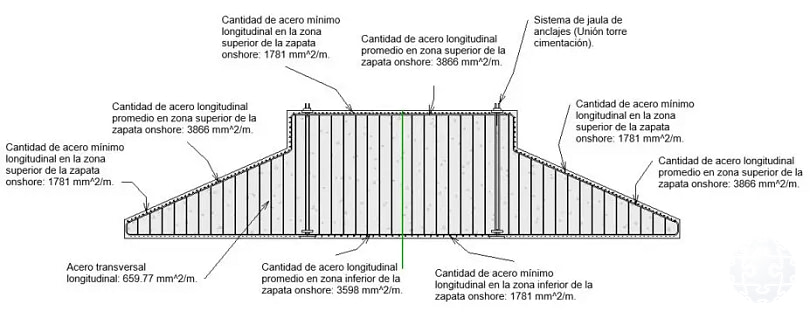
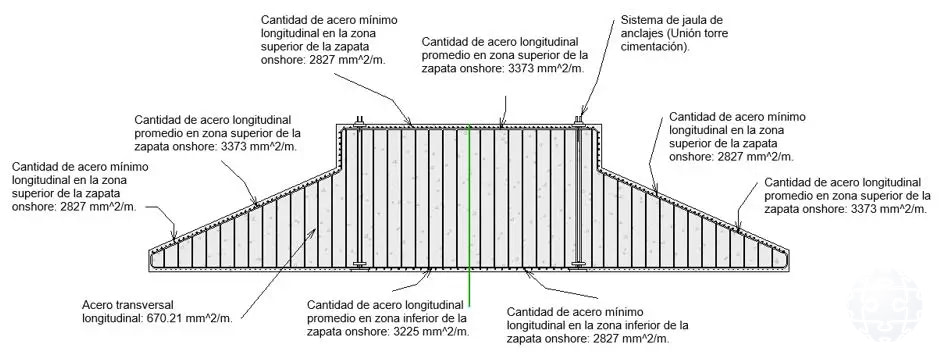
Figura 12: Acero de refuerzo requerido (Enfoque ACI).
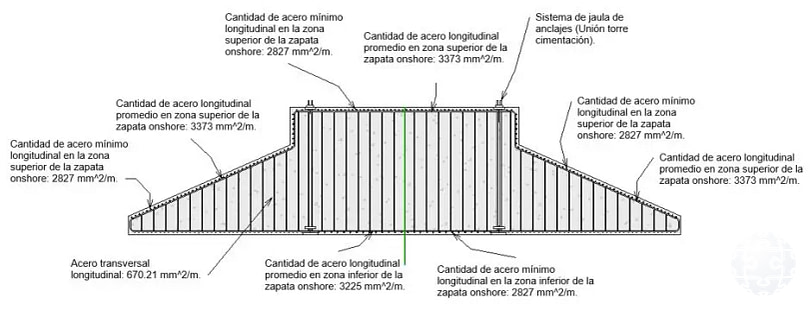
Figura 13: Figura 13: Acero de refuerzo requerido (Enfoque EN 1992-1-1:2004).
Conclusiones
El diseño de cimentaciones para turbinas eólicas es una disciplina cada vez más demandada, impulsada por el crecimiento sostenido del sector de las energías renovables. Dominar los métodos de análisis geotécnico y estructural aplicados a este tipo de cimentaciones representa una ventaja competitiva para los ingenieros que deseen especializarse en un área con alta proyección profesional.
Al inscribirte en nuestro “Curso Cimentaciones para Turbinas Eólicas (Onshore y Offshore)”, adquirirás los conocimientos necesarios para abordar proyectos tanto Onshore como Offshore, participar activamente en procesos de inspección y construcción, y aplicar con solvencia la normativa internacional vigente.
Referencias
•American Concrete Institute (ACI). Building Code Requirements for Structural Concrete. ACI Code 318-25.
•Muzofa, T.D. (2017). Optimisation of Wind Turbine Foundations. (Tesis de Maestría Stellenbosch University).
•Kuchma D (1998-2004). Cast (Computer Aided Strut and tie). Universidad de Illinois.
•ACI PRC-445.2-21. Strut-and-Tie Method Guidelines.
•DNV GL. (2016a). Support Structures for wind Turbines (DNVGL-ST-0126).
•IEC (2020). Wind Energy Generation System – Part 6: Tower and Foundation Design Requirements (IEC61400-6).
•Europan Union. (2004). Eurocode 2: Design of concrete structures. (EN 1992-1-1:2004).
•Salah El-Din E. El-Metwally (2018). Structural concrete. Strut and tie Models for Unified Design.
Durante el curso el participante podrá abordar el estado del arte en los procesos de diseño y construcción de cimentaciones para turbinas eólicas, tanto para desarrollos offshore como en tierra firme, podrá desarrollar el diseño geotécnico y estructural de las cimentaciones teniendo en cuenta los fenómenos de interacción suelo-estructura que influyen en la respuesta global del sistema.